Procedure

1. Array should be a sorted array.
2. Find the middle element
3. if the target is greater than the middle element -> search in the right
4. else -> search in the left (In an Ascending sorted array)
5. if middle element is equal to target element -> answer found
6. if (Start >End) -> element not found.

Why Binary Search?

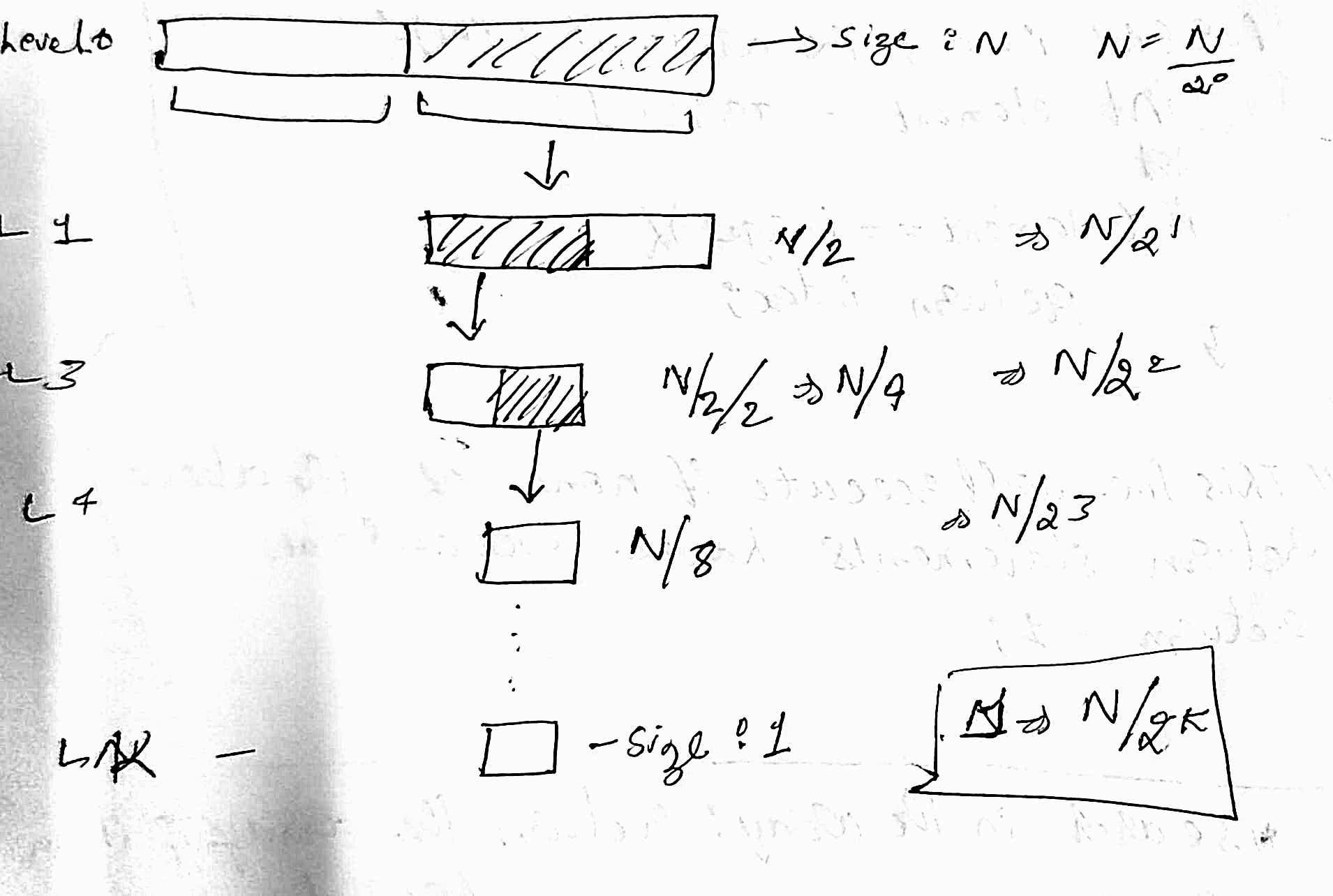
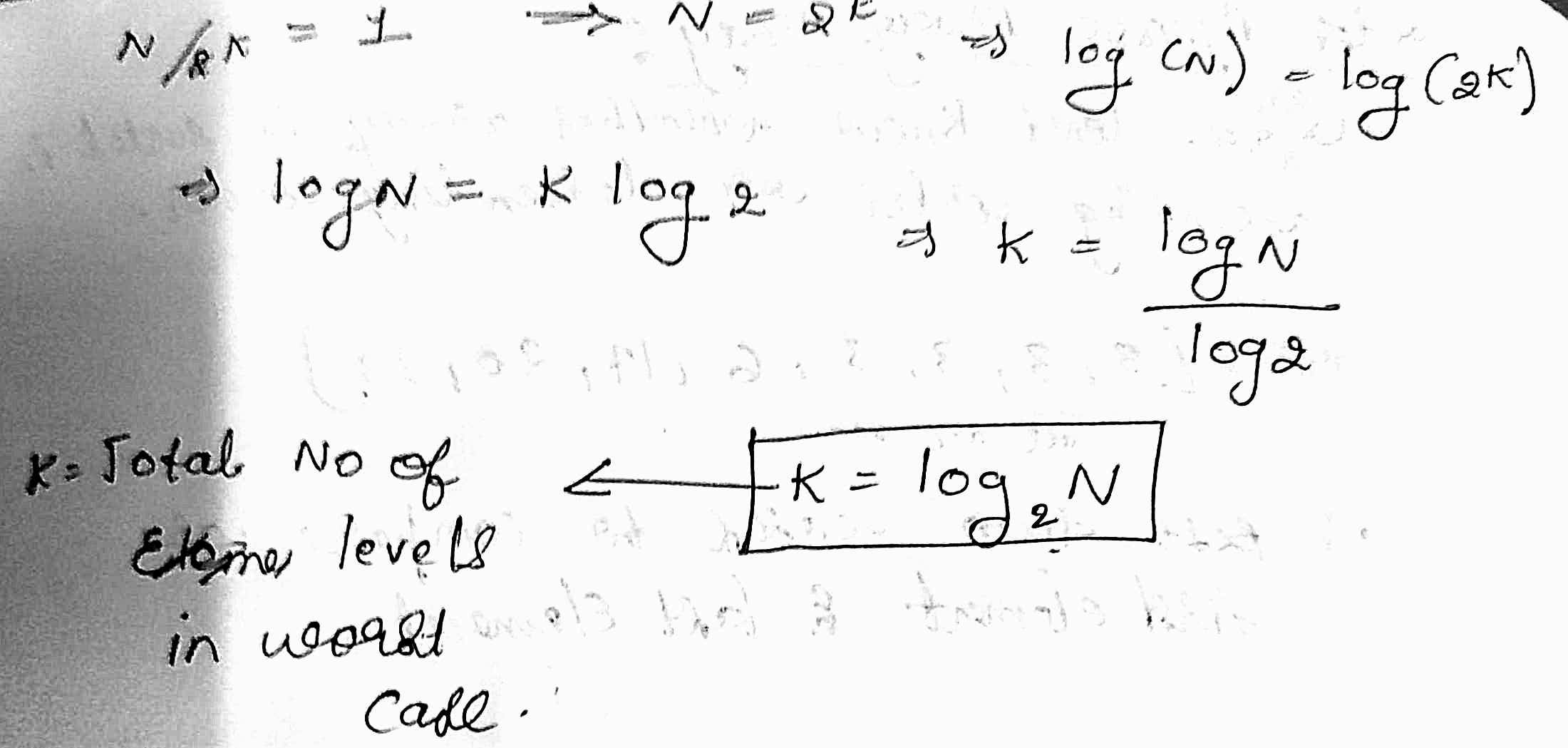
ex: Search in a sorted array of million elements

Worst case :

• Linear search: 1 million comparisons
• Binary Search: K=log(base 2)(10^6)=20 comparisons(approximately)

To calculate mid element :

mid = (start + end)/2 -> but in this case (start + end) may exceed integer range value

so optimized solution is :

mid = start + (end-start)/2

Code for Binary Search

//binary search in an sorted array in ascending order
    static int binarysearch(int[] arr,int target){
        int start=0;
        int end= arr.length-1;

        //to find the  element
        while (start<=end){
            int mid = start+(end-start)/2; //optimised mid

            if (arr[mid] > target) { //search in the left
                end = mid-1;
            }
            else if(arr[mid]<target){ //search in the right
                start=mid+1;
            }
            else{// arr[mid] == target
                return mid;
            }
        }

        //if element is not found
        return -1;
    }

Order Agnostic Binary Array

->When we don't know whether our array is sorted in ascending order or descending order.

Two find whether an array is sorted in ascending order or descending order, we have to compare two different elements:

->so best Two elements are the first element and last element.

Code for Order Agnostic Binary Array

static int orderAgnosticBS(int[] arr,int target){
        int start=0;
        int end= arr.length-1;

        boolean isAsc;
        isAsc= arr[end] > arr[start];

        //to find the  element
        while (start<=end){
            int mid = start+(end-start)/2; //optimised mid

            if(arr[mid]==target){
                return mid;
            }

            if(isAsc){//if array is sorted in ascending order
                if (arr[mid] > target) {
                    end = mid-1;
                }
                else {
                    start=mid+1;
                }
            }
            else{//if array is sorted in descending order
                if (arr[mid] < target) {
                    end = mid-1;
                }
                else {
                    start=mid+1;
                }
            }

        }//end while loop

        //if element is not found
        return -1;
    }

Source : [youtu.be/f6UU7V3szVw]